Vectors - Cross Product

Description:

The Concept

There are only three ways in which Physical Quantities could be multiplied to each other −

Scalar multiplied to a Scalar

Because both the quantities carry just the magnitude, they can be multiplied by the rules of standard multiplication.

Scalar multiplied to a Vector

We have studied this in the previous video of Terminologies and Basic Properties.

The magnitude of the vector gets multiplied to the scalar.

Direction remains unaffected.

Vector multiplied to a Vector

Two products are defined for multiplication of a vector with another vector.

Dot Product which is also called Scalar Product

Cross Product which is also called Vector Product

In this topic, we will discuss Cross product in detail.

Cross Product

Cross product between two vectors is defined as −

a→ x b→ = ab sin θ n̂

It can also be written as −

a→×b→ = |a|→|b|→ sin θ n̂ [We know that |a|→ or a, both represent the magnitude of a→]

Method to find the dot product

Consider the two vectors, a→ and b→.

Two Vector Form

Place them in a way such that their tails coincide, just like we do while using Parallelogram Law.

Tails dot Product

To calculate the magnitude of the resultant P→ = a→×b→, use the equation of cross product −

|P|→ = |a→xb→| = ab sin θ

To calculate the direction of resultant, one needs to understand Right Hand Thumb Rule.

Right Hand Thumb Rule

Right hand should be placed on top of the first vector (in this case, a→ because that is written first) such that the palm faces the second vector.

All fingers should be curled (except the Thumb) towards the second vector.

The direction in which the thumb points gives the direction of n̂ or P→

Right Thumb Rule

Applying Right Hand Thumb Rule in this case −

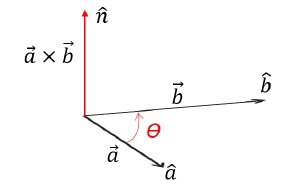
Right Thumb Case

The resultant vector, a→xb→, is perpendicular to both a→ and b→ individually.

Same idea can be expressed by the following equation: a→.n̂ = b→.n̂ = 0 [because the angle between them is 90^o]

Important Points

The direction of the resultant vector is perpendicular to both the original vectors multiplied.

If the angle θ = 0^o or 0 radians,

Vectors are parallel to each other.

the value of sin0 = 0.

he magnitude of cross product is 0 (zero), a→×b→ = 0

If the angle θ = 90^o or θ = π/2 radians,

Vectors are perpendicular to each other.

sin π/2 = 1

This is the maximum value ‘sin θ’ function can take.

The magnitude of cross product is maximum when the angle between them is 90^o or π/2 radians.

|a→xb→| = ab

Properties of Cross Product

Cross product is NOT Commutative

a→xb→ ≠ b→xa→, [due to right hand thumb rule]

Rather, a→xb→ = −(b→xa→)

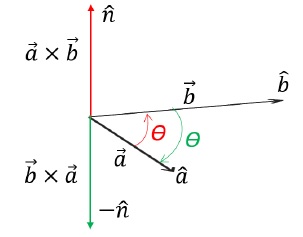
Cross Product

Red vector indicates a→xb→ (red angle θ indicates the correct direction by Right Hand Thumb Rule) while, green vector indicates b→xa→ (green angle θ indicates the correct direction by Right Hand Thumb Rule). It can be clearly seen that a→xb→ = -(b→xa→).

Cross product is Distributive −

a→x(b→ + c→) = a→xb→ + a→xc→

Cross product is NOT Associative −

a→x(b→xc→) ≠ (a→xb→)xc→

Cross product on standard unit vectors

î x î = ĵ x ĵ = k̂ x k̂ = 0 [Vectors are parallel]

î x ĵ = k̂; ĵ x k̂ = î; k̂ x î = ĵ [Right hand thumb rule]

ĵ x î = -k̂; k̂ x ĵ = -î; î x k̂ = -ĵ [Right hand thumb rule]

These results can be observed by applying Right Hand Thumb Rule on coordinate axes.

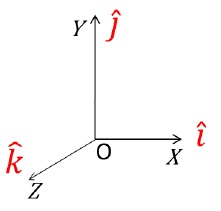
Standard Unit

To memorize these results, following diagram can be used −

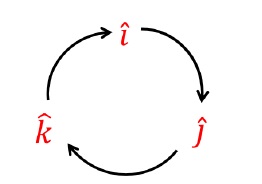
Memorize Result

Above diagram is simple to remember.

î, ĵ and k̂ are drawn respectively in clockwise direction.

They are connected by clockwise turning arrows.

Whenever any two standard unit vectors are crossed, they always yield the third one as the result.

Only the sign of the resultant changes based on which is the first vector.

E.g. î x ĵ = k̂ while, ĵx î = -k̂

Therefore, in the diagram, look for the position of second vector with respect to the first.

If its placed clockwise, the resultant will have positive sign.

Illustration −

ĵ x k̂ = + î [k̂ is situated clockwise to ĵ. Hence, the result is positive î]

î x k̂ = − ĵ [k̂ is situated anti-clockwise to î. Hence, the result is negative ĵ]

Cross Product involving two vectors in component form – Standard Method

Here, a→ = (a_x î + a_y ĵ + a_z k̂)

Also, b→ = (b_x î + b_y ĵ + b_z k̂)

Therefore, S→ = a→ x b→, implies,

P = (a_x î + a_y ĵ + a_z k̂) x (b_x î + b_y ĵ + b_z k̂)

P = (a_xb_x) î x î + (a_xb_y) î x ĵ + (a_xb_z) î x k̂ + (a_yb_x) ĵ x î + (a_yb_y) ĵ x ĵ + (a_yb_z) ĵ x k̂ + (a_zb_x) k̂ x î + (a_zb_y) k̂ x ĵ + (a_zb_z) k̂ x k̂

Using the diagram below,
î x î = 0; î x ĵ = + k̂; î x k̂ = - ĵ; ĵ x î = - k̂; ĵ x ĵ = 0; ĵ x k̂ = î; k̂ x î = ĵ; k̂ x ĵ = - î; k̂ x k̂ = 0

P→ = (a_xb_y) k̂ + (a_xb_z) (- ĵ) + (a_yb_x) (- k̂) + (a_yb_z) î + (a_zb_x) ĵ + (a_zb_y) (- î)

P→ = (a_yb_z - a_zb_y) î + (a_zb_x - a_xb_z) ĵ + (a_xb_y - a_yb_x) k̂

Cross Product involving two vectors in component form – Determinant Method

As a student, you will study about determinants in detail in Mathematics.

For now, let’s try and understand basic approach of solving a determinant and its usefulness in calculating cross product with speed.

Let’s say, a→ = (a_x î + a_y ĵ + a_z k̂)

Also, b→ = (b_x î + b_y ĵ + b_z k̂)

A determinant should be created in the following way −

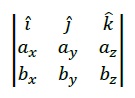
Determinant

Please watch the video to understand how to solve a determinant step-by-step.

After knowing the method, one can get the cross product value instantly as −
- P→ = (a_yb_z - a_zb_y) î - (a_xb_z - a_zb_x) ĵ + (a_xb_y - a_yb_x) k̂

Previous Page Next Page