Vectors - Resolution

Description:

Concept of Resolution

The concept of resolution could be understood in contrast to the concept of addition.

Let’s say a→ and b→ are added to get S→. This is the process of addition.

Now, S→ is broken to obtain a→ and b→ back. This is the process of resolution.

A vector can be resolved into many different vectors. Understand this with following example −

Let’s say two numbers 4 and 6, are added to obtain 10; 4 + 6 = 10

Now 10 is broken or resolved, and the numbers added are obtained back; 10 = 4 + 6

But, 10 can also be resolved into many other numbers like;
10 = 5 + 5;
10 = 3 + 7;
10 = 2 + 8;
10 = 1 + 9;
10 = 2 + 5 + 3;
10 = 1 + 2 + 3 +4; etc

In the same fashion, one can understand that a vector can essentially be resolved (broken) to obtain multiple vectors of different magnitudes and directions.

In Physics, vectors would be mainly resolved only along the coordinate axes, X, Y and Z.

Resolving a vector along X and Y axis

Draw the vector to be resolved on an X-Y plane.

Label and create the constructions on figure as shown below.

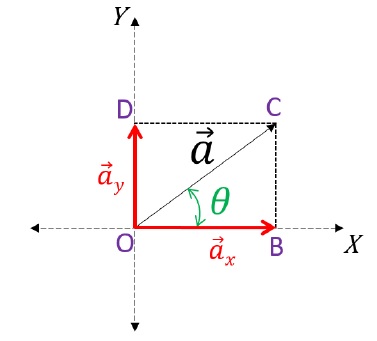
Resolving Construction

One can see that the setup appears to be of the Parallelogram law of vector addition. Here, two vectors a→_x and a→_y appear to be added to obtain a→.

Therefore, we can say that a→_x and a→_y are the resolved output of a→. (Because a→ has been broken back to its components)

a→_x is the x-component and a→_y is the y-component of a→.

To find the magnitudes of each component,

In △OBC:

cos θ = OB/OC; Therefore, OB = OC cos θ

Therefore, |a_x|→ = |a|→ cos θ [Magnitude of x-component]

sin θ = BC/OC; Therefore, BC = OC sin θ; Also, BC = OD(Opposite sides of Rectangle);

Therefore, |a_y|→ = |a|→ sin θ [Magnitude of y-component]

Note

General Rule of Thumb −

The subtended angle will always touch one of the components. Whichever component the given angle touches or the given angle is subtended with, that will be the cos component of the given vector. The other is automatically the sin component.

Unit Vectors along co-ordinate axes

There are special unit vectors designated by convention for the co-ordinate axes.

î, ĵ, and k̂, respectively represent X, Y, and Z axes.

By property of unit vectors, |î| = |ĵ| = |k̂| = 1

Writing Vectors in component form (Using coordinate axes unit vectors)

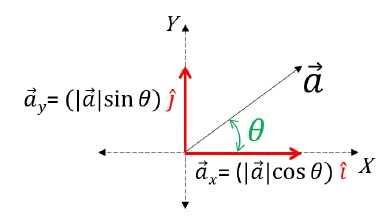
Writing Vector

We know that a vector can be expressed as a product of its magnitude and direction. Therefore,

a_x→ = |a_x|→ î;
Magnitude of a_x→, which is |a_x|→, is multiplied to the direction in which a_x→ lies, which is the direction of x-axis, represented by the unit vector î.

a_y→ = (|a_y|→ sin θ) ĵ;
Magnitude of a_y→, which is |a_y|→, is multiplied to the direction in which a_y→ lies, which is the direction of y-axis, represented by the unit vector ĵ.

Now we know that, a→ = a_x→ + a_y→;

Therefore, a→ = (|a|→ cos θ) î + (|a|→ sin θ) ĵ [Final Component Form]

Addition and Subtraction of Vectors in component form (Expressed as unit vectors)

Consider the following figure −

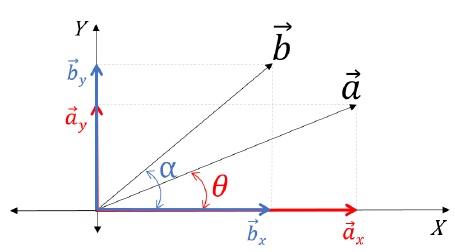
Component Form

Expressing a→ in component form,

a→ = a_x→ + a_y→;

a→ = |a_x|→ î + |a_y|→ ĵ;

a→ = |a|→ cos θ î + |a|→ sin θ ĵ

Expressing b→ in component form,

b→ = b_x + b_y→;

b→ = |b_x|→ î + |b_y|→ ĵ

b→ = |b|cos α î + |b|→ sin α ĵ

Operation, S→ = a→ + b→;

S→ = a→ + b→ = (|a_x|→ î + |a_y|→ ĵ) + (|b_x|→ î + |b_y|→ ĵ);

This implies, S→ = (|a_x|→ + |b_x|→) î + (|a_y|→ + |b_y|→) ĵ;

Hence, S→ = (|a|→ cos θ + |b|→ cos α) î + (|a|→ sin θ + |b|→ sin α)ĵ [Final Sum]

Operation, S→ = a→ − b→;

S→ = a→ + b→ = (|a_x|→ î - |a_y|→ ĵ) + (|b_x|→ î - |b_y|→ ĵ);

This implies, S→ = (|a_x|→ - |b_x|→) î + (|a_y|→ - |b_y|→) ĵ;

Hence, S→ = (|a|→ cos θ - |b|→ cos α) î + (|a|→ sin θ - |b|→ sin α)ĵ [Final Difference]

Previous Page Next Page