Vectors - Dot Product

Description:

The Concept

There are only three ways in which Physical Quantities could be multiplied to each other −

Scalar multiplied to a Scalar

Because both the quantities carry just the magnitude, they can be multiplied by the rules of standard multiplication.

Scalar multiplied to a Vector

We have studied this in the previous video of Terminologies and Basic Properties.

The magnitude of the vector gets multiplied to the scalar.

Direction remains unaffected.

Vector multiplied to a Vector

Two products are defined for multiplication of a vector with another vector.

Dot Product which is also called Scalar Product

Cross Product which is also called Vector Product

In this topic we will discuss Dot product in detail.

Dot Product

Dot product between two vectors is defined as −

a→.b→ = ab cos θ

It can also be written as −

a→.b→ = |a|→|b|→ cos θ [We know that |a|→ or a, both represent the magnitude of a→]

Method to find the dot product

Consider the two vectors, a→ and b→.

Two Vector Form

Place them in a way such that their tails coincide, just like we do while using Parallelogram Law.

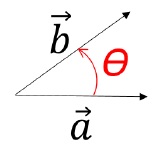
Tails Dot Product

Take the value of ‘θ’ by the right sign convention.

Carry on the dot product operation.

a→.b→ = abcos θ

Important Observations

Result of the dot product is a scalar quantity. For the same reason, there is no resultant in case of the scalar product (The result is not a vector).

If the angle θ = 0^o or 0 radians,

Vectors are parallel to each other.

the value of cos0 = 1.

This is the maximum value ‘cosθ’ function can take.

The dot product is maximum when the angle between them is 0^o or 0 rad. The value is, a→.b→ = ab

If the angle θ = 90^o or θ = π/2 radians,

Vectors are perpendicular to each other.

cos π/2 = 0

The value of dot product is 0 (zero), a→.b→ = 0

Properties of Dot Product

Dot product is Commutative −

a→.b→ = b→.a→(each equal to abcos θ)

Dot product is Distributive

a→.(b→ + c→) = a→.b→ + a→.c→

Associative property is not applicable to dot product.

Same rules can be used on coordinate axis unit vectors, î, ĵ and k̂.

î.î = ĵ.ĵ = k̂. k̂= 1

When a unit vector is multiplied to itself in dot product fashion, the result is always 1.

î.î = |î| |î|cos0 = 1×1×1 = 1
- Magnitude of any unit vector is always 1. Hence, |î| = 1.
- Both are the same unit vectors hence they are parallel to each other. Hence, θ = 0 radians.

î.ĵ = ĵ.k̂ = k̂.î = 0

When one of these unit vectors (î, ĵ or k̂) is multiplied to the other, the result is always 0.
- For example, î.ĵ = |î||ĵ|cos π/2 = 1×1×0 = 0
- Magnitude of any unit vector is always 1. Hence, |î| = 1.
- î, ĵ and k̂ are mutually perpendicular to each other. Hence, θ = π/2 radians.

Also, because dot product is commutative, ĵ.î = k̂.ĵ = î.k̂ = 0

Dot Product involving two vectors

Here, a→ = (a_x î + a_y ĵ + a_z k̂)

Also,b→ = (b_x î + b_y ĵ + b_z k̂)

Therefore, S→ = a→.b→ implies,

P = (a_x î + a_y ĵ + a_z k̂) . (b_x î + b_y ĵ +b_z k̂)

P = (a_xb_x) î.î + (a_yb_y) î.ĵ + (a_xb_z) î.k̂ + (a_yb_x) ĵ.î + (a_yb_y) ĵ.ĵ + (a_yb_z) ĵ.k̂ + (a_zb_x) k̂.î + (a_zb_y) k̂.ĵ + (a_zb_z) k̂.k̂

We know that î.î = ĵ.ĵ = k̂.k̂ = 1 and every other combination of î, ĵ and k̂ gives a 0(zero) answer.

Hence, P = a_xb_x + a_yb_y + a_zb_z

Previous Page Next Page