E-R Graph for Charged Shell of Non Conducting Sphere
Description:
We know that in case of a shell, The electric field outside the shell is −
Eoutside = 14πε0 qr2
Where ‘r’ is the distance of point from the centre of the shell where electric field is to be measured. ‘r’ is a variable quantity.
When ‘r’ decreases and reaches to the surface of the shell, where r = R. Where R is the radius of the shell. The value of electric field on the surface reaches to its maximum value.
Esurface = 14πε0 qR2
As we know that electric field E ∝ 1/r2 and ‘r’ on the surface is smaller than the ‘r’ outside the shell,
Esurface > Eoutside
So we conclude that E goes on increasing towards the surface.
Now, To study Electric Field due to charge distributed with in a non conducting sphere.
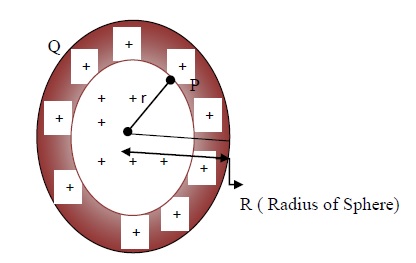
Take a non conducting sphere of radius R, with total charge within the sphere be ‘Q’. In non conducting sphere, its material does not allow charges to come over the surface. So the charges remain distributed within its volume, with volumetric charge density (ρ). We need to calculate electric field due to a non conducting sphere at point ‘P’ which is somewhere inside the sphere at a distance ‘r’ from its centre where ‘r < R’ using gauss theorem.
Step 1
Consider a Gaussian surface in form of a concentric sphere of radius ‘r’ so that it passes through ‘P’. E is radial (perpendicular to charged surface) with same distance to Gaussian surface. It is symmetrical at every point and area vector A makes 0. At every point.
Step 2
We know
∮ E.dScos θ = q/ε0
On putting the value of θ = 0. In LHS We get −
∮ E.dScos θ = E ∮ dS
When the complete area of Gaussian Surface is added up we get 4πr2 so, on integrating within the limit (0-4πr2) we get −
∮ E.dScos θ = E ∮ dS = 4Eπr2
Step 3
Charge within the Gaussian surface −
let the charges inside the Gaussian surface be ‘q’.(As only charges enclosed inside the surface is responsible for creating electric field on the surface)
Charge inside a unit volume = ρ
So charge inside the complete volume of Gaussian Surface (4/3)πr3 = ρ(4/3)πr3
Step 4
Apply Gauss Theorem −
∮ E→.dS→ = q/ε0
Now, putting values in the equation we get −
4Eπr2 = ρ4πr33ε0
So, E = ρr3ε0 ..........(1)
This is the electric field at distance ‘r’ due to charges within a non-conductor. Where r is a variable and E keeps on changing with respect to r. In case of a non conducting sphere, electric field increases with increase in distance from the centre i.e there is a linear relation between distance and electric field.
Converting electric field in terms of Q
Since Q = (4/3)πR3ρ
So, ρ = 3Q4πR3
Putting it in eq (1) We get E = Qr4πε0R3
Now, Eoutside ∝ 1/r2
Electric field outside the surface increases with decrease in distance ‘r’.
Esurface = constant
Electric field on the surface is constant and maximum.
Einside ∝ r
Electric field inside the surface increases linearly with increase in distance ‘r’. So at the centre r = 0 so E = 0
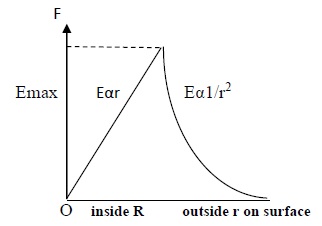
Graph of electric field with reference to distance in case of a non conductor
In graph X axis represents the distance (r) from the centre of the shell and Y axis represents electric field (E).
Point ‘O’ is the origin and represents the centre of the non conducting sphere.
In X axis, we take a point ‘R’ such that the distance OR represents the radius of the sphere.
Right side of point R, represents the outer surface of the sphere.
Electric field in Y axis can go upto a certain maximum value.
Inside a non conducting sphere, Electric field increases linearly with increase in distance ‘r’. Electric field is always zero at the centre (from eq 3). So the straight line from O to Emax, represents linear increase in electric field.
On the surface of the shell, when distance = R, the electric field is maximum (from eq 2). Represented by a dotted line from R to Emax.
As we move outside the shell, the electric field goes on decreasing with the increase in distance (r) (from eq1, E ∝ 1/r2). Represented by a falling exponential curve.